ML 101 - The Components of a Neural Network

This is article #5 in the “ML 101” series, the purpose of which is to discuss the fundamental concepts of Machine Learning. I want to ensure that all the concepts I might use in the future are clearly defined and explained. One of the most significant issues with the adoption of Machine Learning into the field of finance is the concept of a “black box.” There’s a lot of ambiguity about what happens behind the scenes in many of these models, so I am hoping that, in taking a deep-dive into the theory, we can help dispel some worries we might have about trusting these models.
Introduction
Neural Networks are the poster boy of Deep Learning, a section of Machine Learning characterised by its use of a large number of interwoven computations. The individual computations themselves are relatively straightforward, but it is the complexity in the connections that give them their advanced analytic ability.
The Neuron
The building block of a neural network is the single neuron. The diagram below shows the structure of a neutron with one input.
The input to the neuron is x, which has a weight w associated with it. The weight is the intrinsic parameter, the parameter the model has control over in order to get a better fit for the output. When we pass an input into a neuron, we multiply it by its weight, giving us x * w.
The second element of the input is called the bias. The bias is determined solely by the value b, since the value of the node is 1. The bias adds an element of unpredictability to our model, which helps it generalise and gives our model the flexibility to adapt to different unseen inputs when using testing data.
The combination of the bias and input produces our output y, giving us a formula of w*x + b = y. This should look familiar as a modification of the equation of a straight line, y = mx + c. Neural Networks are made up of tens, hundreds or many even thousands of interconnected neurons, each of which runs its own regression. It’s essentially a regression on steroids.
Multiple Inputs
Naturally, we will not be able to analyse most datasets we come across in the real world using a regression as simple as the diagram above. We will expect to see many more inputs that are combined to estimate the output. This is achieved in a similar way as the neuron with one input.
The formula for the above equation will read x0 * w0 + x1 * w1 + x2 * w2 + b = y.
Layers
Neural networks organise neurons into layers. A layer in which every neuron is connected to every other neuron in its next layer is called a dense layer.
Through this increasing complexity, neural networks are able to transform data and infer relationships in a variety of complex ways. As we add more layers and nodes to our network, this complexity increases.
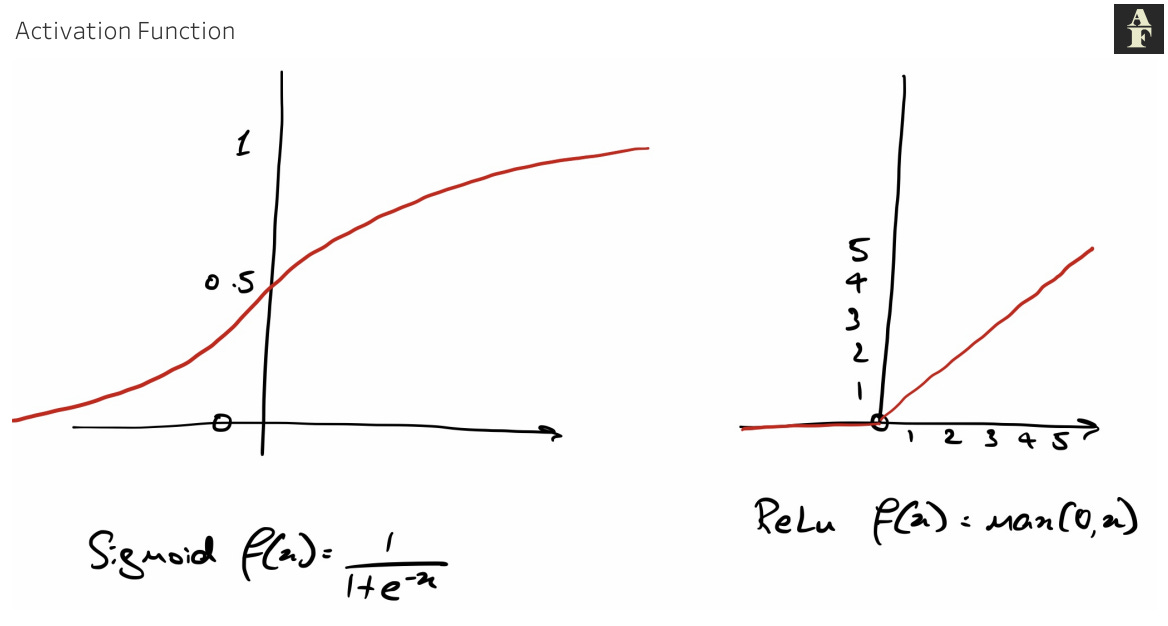
Activation Function
Currently our model is only good for predicting linear relationships in our data. In the previous diagram, there’s no benefit to running this neural network as opposed to a series of regressions.
Neural Networks provide a solution to this in two ways. The first is the ability to add more layers to our network between the input and output, known as hidden layers. Each of these hidden layers will have a predefined number of nodes and this added complexity starts to separate the neural network from its regression counterpart.
The second way that Neural Networks add complexity is through the introduction of an activation function at every node that isn’t an input or output. If you’re unfamiliar with the term, I would definitely check out a previous article I wrote on Linear Classification which looks at activation functions in far more depth, but to summarise from there, an activation function is a function that transforms our input data using a non linear method. Sigmoid and ReLu are the most commonly used activation functions.
The fact that both of these models are non linear means that we add another element of adaptability to our model, because it can now predict classes that do not have linear decision boundaries or approximate non linear functions. In the simplest of terms, without an activation function, neural networks can only learn linear relationships. The fitting of an object as simple as an x² curve would not be possible without the introduction of an activation function.
So the role of a neuron in a hidden layer is to take the sum of the products of the inputs and their weights and pass this value into an activation function. This will then be the value passed as the input to the next neuron, be it another hidden neuron or the output.
Optimising Weights
When a Neural Network is initialised, its weights are randomly assigned. The power of the neural network comes from its access to a huge amount of control over the data, through the adjusting of these weights. The network iteratively adjusts weights and measures performance, continuing this procedure until the predictions are sufficiently accurate or another stopping criterion is reached.
The accuracy of our predictions are determined by a loss function. Also known as a cost function, this function will compare the model output with the actual outputs and determine how bad our model is in estimating our dataset. Essentially we provide the model a function that it aims to minimise and it does this through the incremental tweaking of weights.
A common metric for a loss function is Mean Absolute Error, MAE. This measures the sum of the absolute vertical differences between the estimates and their actual values.
The job of finding the best set of weights is conducted by the optimiser. In neural networks, the optimisation method used is stochastic gradient descent.
Every time period, or epoch, the stochastic gradient descent algorithm will repeat a certain set of steps in order to find the best weights.
Start with some initial value for the weights
Keep updating weights that we know will reduce the cost function
Stop when we have reached the minimum error on our dataset
Gradient Descent requires a differentiable algorithm, because when we come to finding the minimum value, we do this by calculating the gradient of our current position and then deciding which direction to move to get to our gradient of 0. We know that the point at which the gradient of our error function is equal to 0 is the minimum point on the curve, as the diagrams below show.
The algorithm we iterate over, step 2 of our gradient descent algorithm, takes our current weight and subtracts from it the differentiated cost function multiplied by what is called a learning rate, the size of which determines how quickly we converge to or diverge from the minimum value. I have an explanation in greater detail on the process of gradient descent in my article on Linear Regression.
Over and Underfitting
Overfitting and Underfitting are two of the most important concepts of machine learning, because they can help give you an idea of whether your ML algorithm is capable of its true purpose, being unleashed to the world and encountering new unseen data.
Mathematically, overfitting is defined as the situation where the accuracy on your training data is greater than the accuracy on your testing data. Underfitting is generally defined as poor performance on both the training and testing side.
So what do these two actually tell us about our model? Well, in the case of overfitting, we can essentially infer that our model does not generalise well to unseen data. It has taken the training data and instead of finding these complex, sophisticated relationships we are looking for, it has built a rigid framework based on the observed behaviour, taking the training data as gospel. This model doesn’t have any predictive power, because it has attached itself too strongly to the initial data it was provided, instead of trying to generalise and adapt to slightly different datasets.
In the case of underfitting, we find the opposite, that our model has not attached itself to the data at all. Similar to before, the model has been unable to find strong relationships, but in this case, it has generated loose rules to provide crude estimations of the data, rather than anything concrete. An underfit model will therefore also perform poorly on training data because of its lack of understanding of the relationships between the variables.