ML 101 - Model Selection & Evaluation

This is article #6 in the “ML 101” series, the purpose of which is to discuss the fundamental concepts of Machine Learning. I want to ensure that all the concepts I might use in the future are clearly defined and explained. One of the most significant issues with the adoption of Machine Learning into the field of finance is the concept of a “black box.” There’s a lot of ambiguity about what happens behind the scenes in many of these models, so I am hoping that, in taking a deep-dive into the theory, we can help dispel some worries we might have about trusting these models.
Model Selection and Evaluation is a hugely important procedure in the machine learning workflow. This is the section of our workflow in which we will analyse our model. We look at more insightful statistics of its performance and decide what actions to take in order to improve this model. This step is usually the difference between a model that performs well and a model that performs very well. When we evaluate our model, we gain a greater insight into what it predicts well and what it doesn’t and this helps us turn it from a model that predicts our dataset with a 65% accuracy level to closer to 80% or 90%.
Metrics and Scoring
Let’s say we have two hypothesis for a task, h(x) and h’(x). How would we know which one is better. Well from a high level perspective, we might take the following steps:
Measure the accuracy of both hypotheses
Determine whether there is any statistical significance between the two results. If there is, select the better performing hypothesis. If not, we cannot say with any statistical certainty that either h(x) or h’(x) is better.
When we have a classification task, we will consider the accuracy of our model by its ability to assign an instance to its correct class. Consider this on a binary level. We have two classes, 1 and 0. We would classify a correct prediction therefore as being when the model classifies a class 1 instance as class 1, or a class 0 instance as class 0. Assuming our 1 class as being the ‘Positive class’ and the 0 class being the ‘Negative class’, we can build a table that outlines all the possibilities our model might produce.
We also have names for these classifications. Our True Positive and True Negative are our correct classifications, as we can see in both cases, the actual class and the predicted class are the same. The other two classes, in which the model predicts incorrectly, can be explained as follows:
False Positive — when the model predicts 1, but the actual class is 0, also known as Type I Error
False Negative — when the model predicts 0, but the actual class is 1, also known as Type II Error
When we take a series of instances and populate the above table with frequencies of how often we observe each classification, we have produced what is known as a confusion matrix. This is a good method to begin evaluating a hypothesis that goes a little bit further than a simple accuracy rate. With this confusion matrix, we can define the accuracy rate and we can also define a few other metrics to see how well our model is performing. We use the shortened abbreviations False Positive (FP), False Negative (FN), True Positive (TP) and True Negative (TN).
Below is an example of a 3 class confusion matrix and how we transform this into recall, precision and f1 figures for each class. It’s important to mention here that in the case of more than 2 classes, our 0 class will be all classes that are not our 1 class.
An Example
These additional metrics are useful because they give us more insight into the behaviour of a classifier. For example, consider the following two classifiers:
With a simple accuracy measurement, we would be inclined to say that Classifier B is the better classifier, because its accuracy rate is higher at 0.75 vs 0.50. However, when we introduce our other metrics, we can calculate the the precision and recall of classifier B is 0. The precision and recall of classifier A are 0.25 and 0.50 respectively. From this information, we see a completely different picture. Classifier B is relatively useless, particularly because it cannot predict any class 1 examples and the precision and recall reflect this where the accuracy figure does not.
One more metric that is often used in understanding how well a classifier performs is the Receiver Operator Characteristic (ROC) curves. These plot the True Positive rate on the y axis vs the False Positive rate on the x axis. We generate these data points by adjusting the decision threshold of our classifier (i.e. for a probability classifier, we would change the threshold from the default 0.5, to 0.6, 0.7, etc, where if the predicted value is greater then this threshold we assign class 1, otherwise we assign class 0).
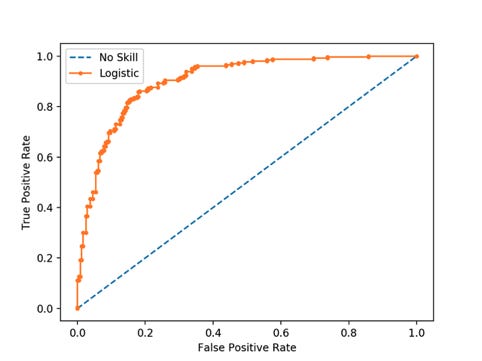
We generally consider the greater the area under the curve, the greater the model is, because it informs us that this model has the opportunity to return a high TP rate with the correct threshold. Typical ROC curves will also plot a dotted line from (0,0) to (1,1) which represent the performance of a random classifier (one that predicts the correct class 50% of the time).
Overfitting
Overfitting is a key consideration when looking at the quality of a model. Overfitting occurs when we have a hypothesis that performs significantly better on its training data examples than it does on the test data examples. This is an extremely important concept in machine learning, because overfitting is one of the main features we want to avoid. For a machine learning model to be robust and effective in the ‘real world’, it needs to be able to predict unseen data well, it needs to be able to generalise. Overfitting essentially prevents generalisation and presents us with model that initially looks great because it fits to our training data very well, but what we ultimately find is that the model will have fit to the training data too well. The model has essentially not identified general relationships in the data, but instead has focused on figuring out exactly how to predict this one sample set. This can happen for a number of reasons:
The learning process is allowed to continue for too long
The examples int he training set are not an accurate representation of the test set and therefore also of the wider picture
Some features in the dataset are uninformative and so the model is distracted, assigning weights to these values that don’t realise any positive value
Cross Validation
Cross Validation can be considered under the model improvement section. It is a particularly useful method for smaller datasets. Splitting our data into training and test data will reduce the number of samples that our model receives to train on. When we have a relatively small number of instances, this can have a large impact on the performance of our model because it does not have enough data points to study relationships and build reliable and robust coefficients. In addition to this, we make an assumption here that our training data has a similar relationship between the variables that our testing data does, because only in this situation will we actually be able to generate a reasonable model that can predict with a good level of accuracy on unseen data.
The solution that we can turn to here is a method called cross validation. In cross validation, we run our modelling process on different subsets of the data to get multiple measures of model quality. Consider the following dataset, split into 5 sections, called folds.
In Experiment 1, we use the first fold as our testing set and everything else as training data. In Experiment 2, we use data from the second fold, which we also call the “holdout set” and use the remaining 80% to train the model. We repeat this process, using every fold once as the holdout set so that 100% of the data is used as holdout and training at some point. The output from a cross validation model will be the average accuracy from all k folds (where k is 5 in the example above), which should give us a more representative figure of the actual performance of our model.
Cross validation can give us a more accurate measure of model quality, however it can take a long time because it estimates multiple models. For small datasets, where the extra computational burden isn’t a large issue, we can run cross validation.






