ML 101 - Data Transformation Methodologies

This is article #8 in the “ML 101” series, the purpose of which is to discuss the fundamental concepts of Machine Learning. I want to ensure that all the concepts I might use in the future are clearly defined and explained. One of the most significant issues with the adoption of Machine Learning into the field of finance is the concept of a “black box.” There’s a lot of ambiguity about what happens behind the scenes in many of these models, so I am hoping that, in taking a deep-dive into the theory, we can help dispel some worries we might have about trusting these models.
Machine Learning is the development of algorithms that learn from information. They study relationships within the data presented to them and use this to then predict the nature of unseen outcomes. In the same way that we do as humans, computers learn with experience. It follows this that computers require high quality information for them to make correct assumptions. Because traditional machine learning models don’t have the ability to adjust their predictions based on varying data quality, it’s our job as the programmer to ensure that the data is presented well so the models have the best chance at making accurate predictions. We do this in a variety of ways.
Preprocessing
Consider the following dataset:
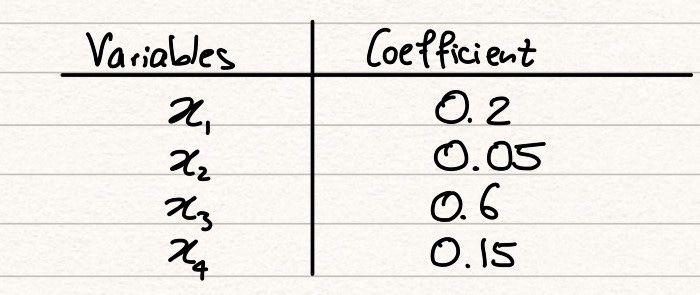
We have 4 explanatory variables, denoted by the xi’s and 1 target variable, y1. In a typical ML problem, we will want to find a way to explain the target variable by the explanatory variables. The simplest model that we could use for this would be linear regression. Let’s assume we run a simple linear regression and we display the coefficients for each explanatory variable in the table below.
From just an initial view, we might reach the following conclusion from these coefficients:
Variable x3 is the variable that best explains the target value. After this, the order of influence of the variables is x1, then x4, then x2.
This conclusion, however, would be wrong. The reason why this is the case can be understood when we look at the ranges. Whilst x3 has a coefficient 3 times that of x1, the range of x3 is 10 times that of x1. Purely because of this, any x3 value will dominate our regression over x1, simply because the values are larger. The difference in ranges means that the coefficients aren’t comparable and so we can’t make the statement we did before until all our variables are on a level playing field.
This introduces just one need for preprocessing a dataset before it is passed into a model. To make accurate insights, we have just established that we do need the variables to be comparable. In addition to this, large ranges can land up distracting models from the smaller variables that might give us a better explanation of our target.
So how do we fix this? One method is min-maxnormalisation. This method transforms all attributes to lie in the range [0,1] using the following formula:
Min-max normalisation has an issue with outliers, because it includes them in every step of the transformation. If there are significant outliers in our dataset, the min-max normalisation method will constrict the important middle section of our data into a very small range, resulting in the loss of a large amount of information. If we encounter outliers, we need a method that doesn’t use the minimum or maximum of a dataset and for this, we turn to z-scorenormalisation. Z-score normalisation transforms all values to have 0 mean and a standard deviation of 1, a typical normal distribution, using the following formula:
It’s important to choose the correct method of normalising data so that we are keeping our variables comparable, but not reducing them to the points that the key relationships are lost.
Data Reduction
Data reduction involves reducing the volume of data passed onto ML algorithms. Whilst intuitively, this might not make too much sense; we want models to learn from as much information as possible so that they can adapt to any situation, reducing some elements of our input data helps us to de-clutter our information, presenting our model with a clearer view of what we are looking to predict and ensures it isn’t distracted by unnecessary variables.
We might use a discretisation method to turn continuous variables into discrete variables. Discretisation will take a series of data points and a predetermined number of groups and divide the dataset into equal parts, before categorising each point into its respective group. It might be easiest to think of this process in a similar way to how we might generate bins in a histogram. We divide our dataset into x bins and then give each data point a value between 0 and x-1 depending on which bin it fits into.
Generally this is a process we might look to after we have run a model once and evaluated its performance. If we believe that some of our features are adding too much complexity to our model, we might want to simplify them slightly by putting them into groups. In addition to this, if we see strong correlations between our groups and our target variable, this will further indicate the benefits of discretisation. We have to be aware however, that by discretising values, we do remove a lot of information that they present and we have to manage this trade off.
Feature Selection is another method of data reduction and is one of the most important concepts in an ML workflow. Feature Selection is another process we conduct during the evaluation stage of our ML process as we would with discretisation, once we have run a model already and are looking to improve its accuracy. When conducting feature selection, we look for the following conditions in our dataset:
Features with low variance
*Features with low variance provide very little predictive power to our model
* If a value does not change a large amount, it can be considered a fixed value with which clearly we cannot establish any relationship with the target variable
* We want variables to fluctuate a reasonable amount, since it is the variance that provides us with a predictive power
* This is true to an extent however, as high variance within a specific class will cause problems as we will be unable to establish strong inferences between the independent and dependent variablesCorrelated features
* Multiple highly correlated features should not be present in the same dataset
* The issue we have here is that, since our features are related, our model might incorrectly assign coefficients to the variables, weakening how successful our model will be on unseen data
* We might also be assigning greater importance to a certain section of our dataset than is actually true
The importance of understanding your data is unparalleled. ML algorithms can’t find relationships if they don’t exist and they can’t be expected to sift through a huge amount of unnecessary information in order to find the key bits that they need to make good predictions. It’s your classic “needle in a haystack” scenario. GIGO — Garbage In, Garbage Out, always a good abbreviation to remember. If you don’t give your model clear data, it won’t give you clear results.