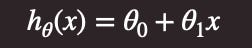ML 101 - An Introduction

The purpose of this article and further ones in the “ML 101” series is to discuss the fundamental concepts of Machine Learning. I want to ensure that all the concepts I might use in the future are clearly defined and explained. One of the most significant issues with the adoption of Machine Learning into the field of finance is the concept of a “black box.” There’s a lot of ambiguity about what happens behind the scenes in many of these models, so I am hoping that, in taking a deep-dive into the theory, we can help dispel some worries we might have about trusting these models.
An Introduction
“[Machine Learning is a] field of study that gives computers the ability to learn without being explicitly programmed.” (Arthur Samuel, 1959)
Arthur Samuel, considered to be the originator of the term “Machine Learning” defined it with the above quote. This definition still stands today but has been developed with time.
“A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.” (Tom Mitchell, 1998)
Tom Mitchell, a computer science professor at Carnegie Mellon University defined a well-structured machine learning problem in 1998 with the above description.
Let’s break both of these quotes down a little further. The key element in both of these definitions is the word “learn” and that’s exactly what the foundation of machine learning is — we want machines to learn without us specifically telling them what should be learned.
Typically, we might want our algorithm to learn how to get from one point to another. That initial point could be a dataset of factors that describe a situation, such as body measurements of a person for example — height, weight, BMI, blood pressure levels etc, and our final point that we want our algorithm to reach could be the life expectancy of that particular person.
Ultimately, what we want to do is to provide the start point and the endpoint of our journey and tell the algorithm to figure out which path to take — that’s what we classify as learning.
This is typical to what we call a “supervised learning” problem — unsupervised learning is the alternative, which does not in fact declare a specific endpoint, but instead tells the algorithm to locate similarities between all of the data points.
The commonality however, is that we do still start without initial dataset and then provide an indication to our algorithm of what we want the output to look like, with varying levels of specification.
In the second definition, we can consider our experience E to be our initial input dataset, the task T to be the instruction that this dataset must be trained to match our output dataset and our performance P as being some form of accuracy metric that essentially informs us of how well a model is performing.
Introducing Functions
So how does all this learning happen? Well, from a high-level view, it happens through the concept of functions. For those that may not be completely familiar, a function is a relation from a set of inputs to a set of possible outputs[1]. If we look at what our definition of machine learning is, the role of the function is exactly what we want our machine to learn, or estimate. We want it to know how to get from our inputs to our outputs, essentially find out what the relation is.
The goal of any machine learning algorithm therefore, is to find the best possible approximation for our function that takes our input variables to as close to our output variables as possible.
The word generalisation is how we apply this to future scenarios. Essentially, what we have built is a relationship between our inputs and outputs. But what if we now give our relationship a new set of inputs? Will it still be able to transform these unseen inputs into the correct set of outputs? Generalisation is the ability to make correct predictions on unseen data.
Ultimately, that is what we want our machine learning algorithms to do. We want them to understand relationships in the data that stand the test of data they haven’t seen before.
The mathematical notation of all the terms described above is noted here:
Let’s look a little further into this concept of functions.
We’ve plotted 4 known data points on a graph and we expect them to have some form of underlying relationship that we are looking to estimate. We’ll call the underlying function f(x) and we have produced 3 basic estimation models, that we call h(x).
The first estimation method is just to draw a line connecting each datapoint. This provides us with a perfect fit for our seen data because we have estimated the exact f(x) value at every x point. This model however has no generalisable properties and if we add an unseen datapoint (the point in red), our model will have no way of estimating this since there is no procedure in place for this x value.
Alternatively, we could use a 3rd order polynomial, which appears to be another good fit for the seen data points. It gathers the general shape of the points and depending on where the unseen datapoint is plotted, this model has the ability to generalise.
A 1st order polynomial in the above case is a straight line. We can see that it doesn’t provide a perfect fit due to the shape of the input data, but again, depending on our x and f(x) relationship, this estimation has the ability to generalise to our unseen data.
This concept is one of the most important to keep in mind about machine learning. We are not looking for the perfect model, because we don’t expect this perfect model to generalise. We’re looking for the best estimation to the data we know in the hope it will also perform well on the data we haven’t exposed the model to yet. In addition to this, the final 2 graphs informs us that the model we choose is always unique to the problem that we are aiming to solve, there is no “one size fits all.”
This brings us to the next conversation — machine learning vs pattern recognition. These are often terms that get grouped together and used interchangeably, but they do actually have unique definitions.
Pattern Recognition and Machine Learning
Machine Learning is learning from experience, the experience being a set of input data that we provide for our algorithm. In machine learning, our experience, task and performance are clearly defined. Machine Learning is also called supervised learning, because we provide both an input and a target output in our data.
Pattern Recognition is the process of finding patterns in our data. It is also called unsupervised learning because, instead of telling the model specifically what the output should be, we ask it to find patterns and relationships within the data. Our experience E will be only feature variables with no target output and our task and performance are more broadly defined because we don’t have a specific path we want our algorithm to follow.
It’s easiest if we consider a couple of examples
Data consisting of 1 feature — age and 1 label — height → univariate supervised learning
Data consisting of 3 features — age, height, gender and 1 label — life expectancy → multivariable supervised learning
Data consisting of 1 feature — a series of prices of the Dow Jones Index, with the aim of classifying the prices into similar groupings → univariate unsupervised learning
Data consisting of 3 features — attributes of a song, tempo, length and key, with the aim of classifying them into groups of similar songs that can hopefully be separable by genre → multivariate unsupervised learning
Supervised Learning
Supervised learning can generally be split into two main categories — classification and regression.
Classification is a machine learning task where we have a discrete set of outcomes. Classification is often binary, meaning that there are two possible options for the outcome, normally yes/no or 1/0. Examples of classification include face detection, smile detection, spam classification.
Regression is a machine learning task where we have a real-valued outcome in a continuous sub-space. Basically, this means that our outcome is a continuous variable, but that it is usually confined to some sort of range. Examples of regression include age estimation, stock value prediction, temperature prediction.
Mathematically we define these as follows:
In the diagram above, the N is the set of all natural numbers. These are all integers greater than 0. The set of natural numbers would look something like {1,2,3,4,…}. The R is the set of all real numbers. This includes all natural numbers, integers, rational and irrational numbers. The only values that the set of real numbers doesn’t include are imaginary numbers, such as i, used to represent the square root of -1, but we don’t encounter these in machine learning so it isn’t something we have to worry about. The important point to note is that classification takes any natural number value, whilst regression takes any real numbered value.
The Components of an ML Problem
We have mentioned the terms features and labels, we will define them now.
Multiple data points make up a dataset. Data points are also called instances. Our machine learning algorithm will use a dataset to create its hypothesis function (estimation function) or find a pattern.
In supervised learning, a data point is made up of a series of inputs, denoted by X, which we call features, and an output, denoted by y, which we call labels. We can group them as tuples in the notation {X,y}.
Labels are what our hypothesis function h(x) tries to predict. Features are what our hypothesis function h(x) will use to predict our label.
It is assumed that there is some implicit relationship between x and y, otherwise we will be attempting to predict an output based on a variable that doesn’t actually provide any relevant information. This will likely create an inaccurate and fairly useless algorithm.
It’s important to note that for a given problem, all data points must have the same fixed length set of features. We can’t pass in different lengths because our algorithm won’t be able to generalise.
So what are the components of a machine learning problem?
Let’s take an example scenario and try to model it.
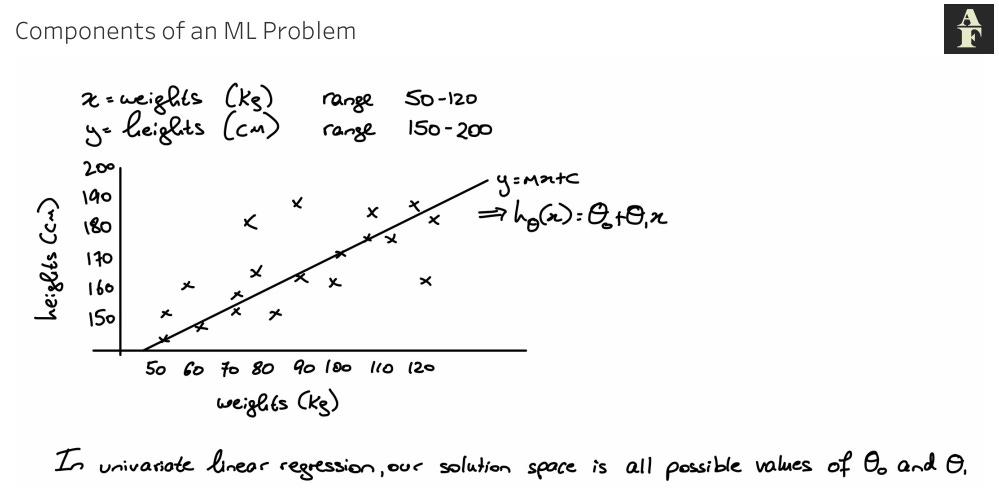
Let’s say that x, our features, are a series of weights of people, measured in kg with a range of 50kg — 120kg. We’ll say that y is the corresponding heights of those people, measured in cm and ranging from 150cm — 200cm. We want to find the best way to use the x value to predict the y. We can start by plotting these points, they might look a little bit like the following diagram. If we decide to use a linear regression to estimate our data, we can plot the straight line estimation on our graph. From graph theory, we know that this line will take the form y = mx + c, where m is the gradient of the line and c is the y-intercept. In ML theory, we convert this into an estimation function:
In univariate linear regression, that is regression with a single x variable, our solution space is all possible values of theta_0 and theta_1.
So the h(x) that is produced by our model is our training algorithm. We are currently in the stage of training our algorithm and we haven’t provided any unseen data yet to see how well it generalises.
We have stated a training algorithm, in the example above, to be the algorithm h(x). The theta parameters are essentially what our algorithm tries to learn. By looking through all our feature and label combinations, it tries to find the best values for theta. The “best” value will be calculated based on whatever our performance metric is, so our algorithm will pick a set of theta values that provide the optimal performance value.
Note that the above example is an extremely simplified version. It is highly likely that our dataset will contain many more than one feature and we may have hundreds or thousands of theta parameters.
Parameters
There are two types of parameters for any machine learning model.
We have intrinsic parameters, which are parameters unique to each model we build. These are the parameters learned by the model such as coefficients in a linear regression like in the example above or weights in an artificial neural network. These are essentially the components of our hypothesis function.
We also have hyper parameters, which can be adjusted by the user and are chosen based on the best performance that they provide. These are far smaller in number than intrinsic parameters. Examples of these are the number of nodes in an artificial neural network, degree of a polynomial for multiple linear regression or the number of features we provide per instance.
Future articles in the ML 101 series will cover other important topics, including Regressions, Neural Networks, Decision Trees and Clustering to name a few. Keep an eye out for those and the articles where we merge these concepts with financial data to build our prediction engines.