Introducing the Weighted Relative Price Strength Metric
Introduction
Timing is key to making trades in the markets. You might know that overall sentiment is low, but once you have the fundamentals, you need to back this up with technical analysis to make sure you catch an asset the end of its pullback as opposed to the start of one. This avoids you starting your trade in the red for a prolonged period of time before it begins to turn in your favour or in many cases, pulling out of the trade too early due to fear that the market will continue to go against you.
In the coming articles, I will continue to describe methods I am working on to help us predict these turning points in the markets. These will range from algorithmic models, to metrics and interactive tools that use candlestick patterns to predict tops or bottoms.
For this article, I want to introduce the WRPS Metric - the Weighted Relative Price Strength. This is a relatively straightforward metric and to sum it up in one sentence, this metric uses the current price as a weighted fraction of past prices to represent the position of the current price. It’s a relatively simple concept and it’s not perfect by any means, but the Proof of Concept below will show that there certainly is some scope for this addition to our analytics. I do anticipate, however, that as we continue this deep dive into financial analytics, this will be a metric that will slowly recede into the background as we find benefits to more involved calculations. So that we never lose track of the bigger picture, simplicity and clarity of thought is always something to have in the back of our mind when doing any form of analysis, but when we are dealing with a dataset as complex as the financial markets, there will always be a need to prioritise the more advanced calculations that attempt to capture all the nuances that are thrown at us.
Methodology
The methodology for this metric is relatively simple. We’re taking 4 historical prices, 1, 3, 6 and 12 months before and dividing our current price by each of these values. We then take each value and compute a weighted average depending on how far each price is from our current price.
I’ve included a snipped of the python code below. I call most of my pricing data from yahoo finance, for which we can use the yfinance package. With this, we pull our desired data into a dataframe, calculate our relative prices and then our WRPS metric.
## Import required dependencies
import pandas as pd
import yfinance as yf
## Pull Data
ticker = 'EURUSD=X'
asset = yf.Ticker(ticker)
df = asset.history(period = 'max'[['Open', 'High', 'Low', 'Close']]
## Calculate Relative Price Strengths
# The data does not include weekends, so 1 month prior is 20 # days, 3 months prior is 60 days etc.
df['1 Month RPS'] = df['Close']/df['Close'].shift(20)
df['3 Month RPS'] = df['Close']/df['Close'].shift(60)
df['6 Month RPS'] = df['Close']/df['Close'].shift(126)
df['12 Month RPS'] = df['Close']/df['Close'].shift(252)
## Calculate WRPS
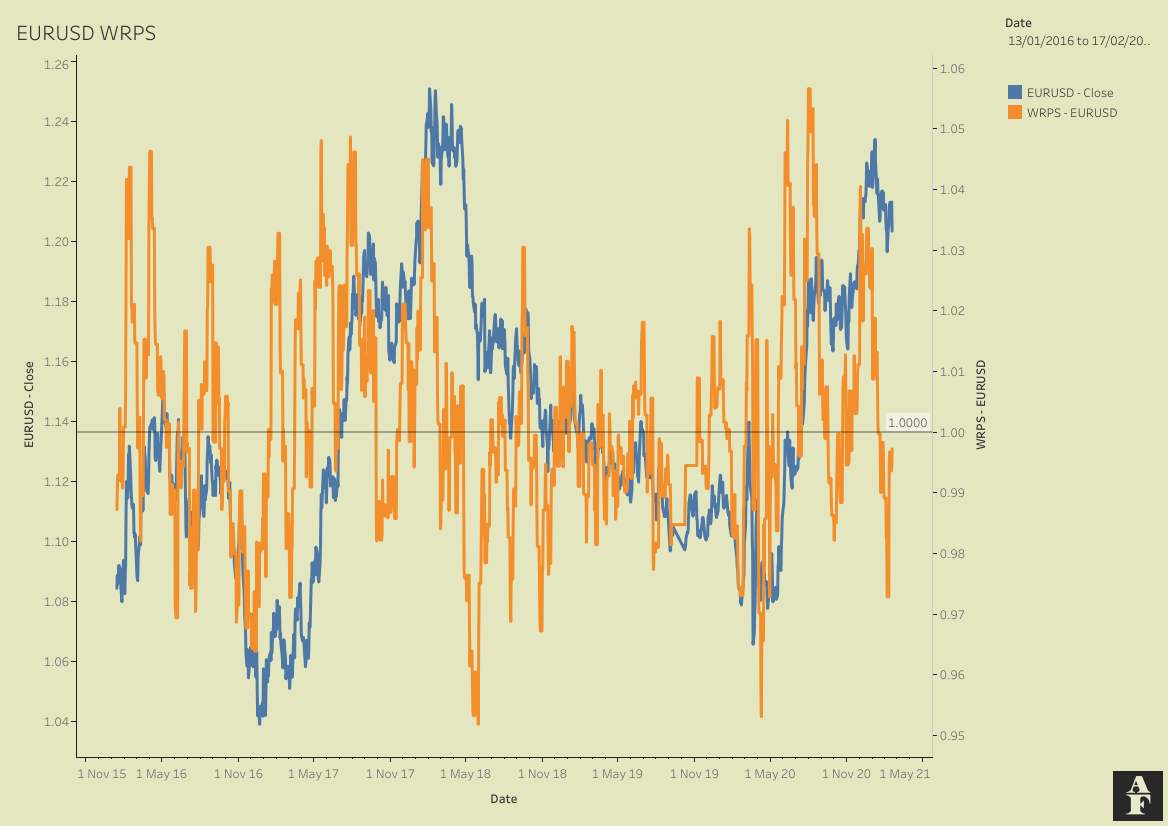
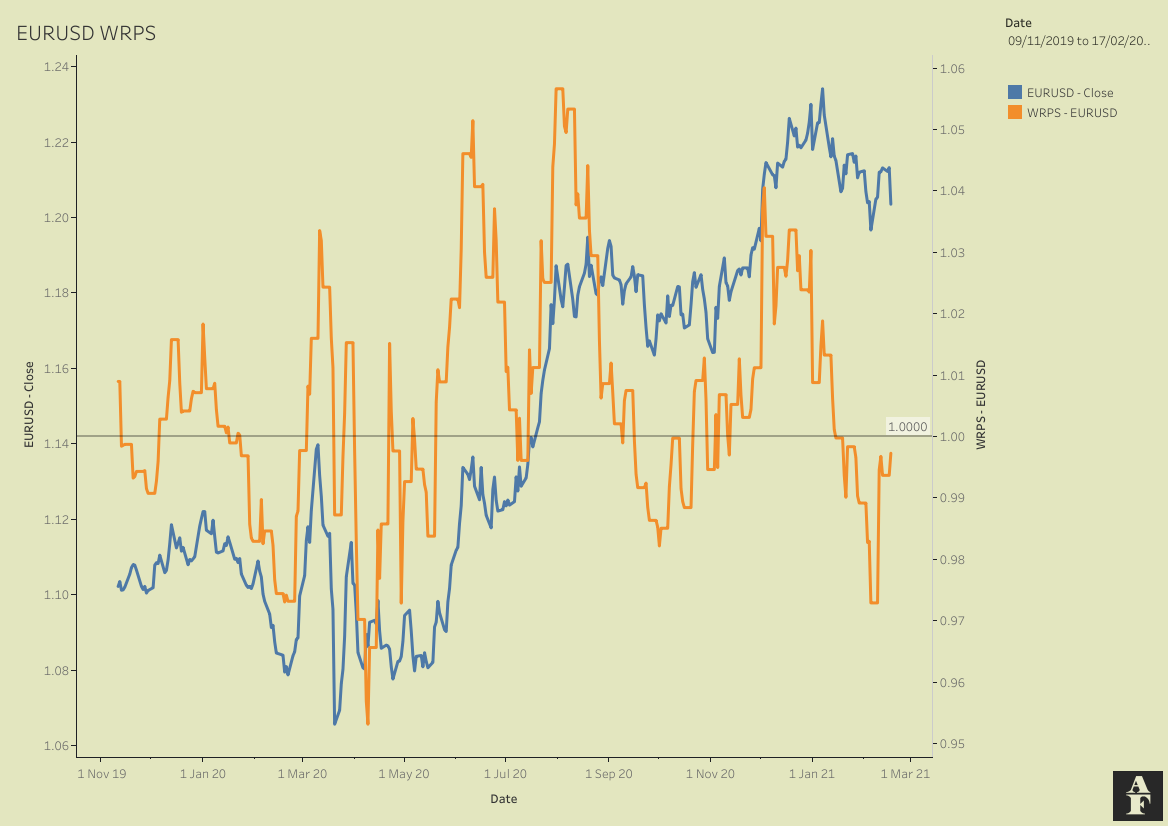
df['WRPS'] = (12*df['1 Month RPS']+ 4*df['3 Month RPS']+ 2*df['6 Month RPS'] + df['1 Month RPS'])/19Yahoo Finance provides daily data for EURUSD since 2003. The chart below visualises this. We’v plotted the closing prices against the WRPS metric on a dual axis. The overall picture doesn’t tell us a huge amount and the PoC below will go into more detail about how we actually check to see if there is any statistical significance here, but a zoomed image of the same chart helps us better understand the visual relationships between these two lines.
Proof of Concept
The Proof of Concept for EURUSD involves an introduction to the ZigZag indicator. This lagging indicator helps us identify minimum and maximum points after they have occurred. It’s not an indicator that we can use in isolation for a trading strategy, because of the significant lag, but it is extremely useful in historical data, in particular due to its accuracy and simplicity. The ZigZag indicator will assign a value to be a minimum or maximum point once the price has moved a predetermined % in the opposite direction. The default value tends to be 5%, so when the price has risen by 5%, the previous lowest point is assigned to be a minimum value and vice versa for the maximum. As you can see, we need a significant change in price to determine these turning points, which is why this strategy cannot be used in trading, but for analysis purposes it is extremely useful.
The chart below shows the same EURUSD closing price, but this time, we have circled our minimum and maximum points, as generated by the ZigZag indicator with a 5% threshold.
My PoC centres around whether there is a statistical difference between the WRPS value we see at minimum points, maximum points and all other points. The table below displays this. We see the 3 different classifications of our data points, followed by the average WRPS value and the standard deviations.
We can see that there is a distinct difference between each of our groups. As soon as our WRPS get close to the 1.04 value, we have seen in the past that we are reaching a maximum point. In the same vein, dropping to a value of 0.95 has given us evidence in the past that we are reaching a minimum point.
An issue that we have with our current collection of turning point values is the lack of data points in order to create distribution estimates. In the EURUSD chart above, we have 24 maximum points and and 25 minimum points. As we continue through time we’ll generate more points and have more accurate representations of our means and standard deviations.
You can view all of the above graphs and more in an interactive format on my Tableau Public account. I will endeavour to update these weekly, but if anyone does notice that the charts are a little bit outdated, please don’t hesitate to drop a mention in the comments and I’ll be sure to re-run the python script as soon as I can. In the link, you’ll find the WRPS metrics for the EURUSD example above and I will be adding the same charts for currencies, equities and commodities in the future. As is standard for all my freely available content, you’re welcome to download and share images of all of these charts and if you have any suggestions for other visualisations you’d like to see, again please don’t hesitate to drop something in the comments.





Hi, great article, thank you for detailed explanation. However could you explain where did you get denominator from in WRPS calculation? I don't fully understand why it is divided by '19'.